Refinement Type Refutations

Refinement Typing

Refinement types are a great way to statically verify properties of programs.

With refinement types, we can annotate a base-type (like Int or Bool) with a logical predicate that restricts the possible values inhabitants of the type may take. For example, in Liquid Haskell we can define the following type for non-zero integers.

type NonZero = Int{v:v /= 0}

We can then use this type to constrain the input and output types of functions. For example, we can specify div as a function that takes a non-zero integer, and returns its first input x divided by its second one, y.

div :: x:Int -> y:NonZero -> Int{v:v == x / y}

The type system then proves at compile-time, that whenever we call div (at runtime), its second argument must indeed be non-zero. This rules out division by zero errors. Great!

Modularity For the Win

What makes refinement types so powerful is their modularity. To check if a program respects all the restrictions imposed by the types – and their refinements – the checker only needs to look at “what’s written on the tin”. That is, the type-checker only works with what we explicitly know from the types, and doesn’t need to perform any additional costly analysis, say, by enumerating program traces.

It’s exactly this modularity that allows refinement types to scale to more advanced features like higher-order functions, datatypes and polymorphism. For example, if we define the type Nat to represent the natural numbers

type Nat = Int{v:0 <= v}

and a function max that returns the larger of two integers

max :: Ord a => a -> a -> a
max x y = if x > y then x else y

we can use the polymorphic function foldr1 to compute the maximum of a (non-empty) list, and the type-checker will automatically verify that the result is indeed a natural number.

foldr1 :: (a -> a -> a) -> [a] -> a
foldr1 = ...

test1 :: Nat
test1 = foldr1 max [4, 3, 2, 1]

It’s worth noting that Liquid Haskell manages to verify this example without further annotations, for example, on the type of foldr1 at this particular call site. This is due to refinement inference which automatically computes solutions for missing refinements.

Summary: Refinement types are a great, and lightweight way to statically check program properties.

When Typing Goes Wrong

But what if we write a function that doesn’t type check? Usually, when we build verification methods, we focus on the case where verification succeeds.

As anyone knows who ever tried to verify a program: success is not the common case! Usually, things go wrong.

Say, we define type Even to represent the even numbers.

type Even = Int{v:v `mod` 2 = 0}

We may now want to repeat our earlier verification success from before, by trying to prove that the maximum of list [4, 3, 2, 1] is even.

test2 :: Even
test2 = foldr1 max [4, 3, 2, 1]

Clearly, this program is correct as the largest number in the list is 4, which is even.

Yet, the program fails to verify with the following cryptic error message from Liquid Haskell. Something is up, but it’s hard to tell what from Liquid Haskell’s error message.

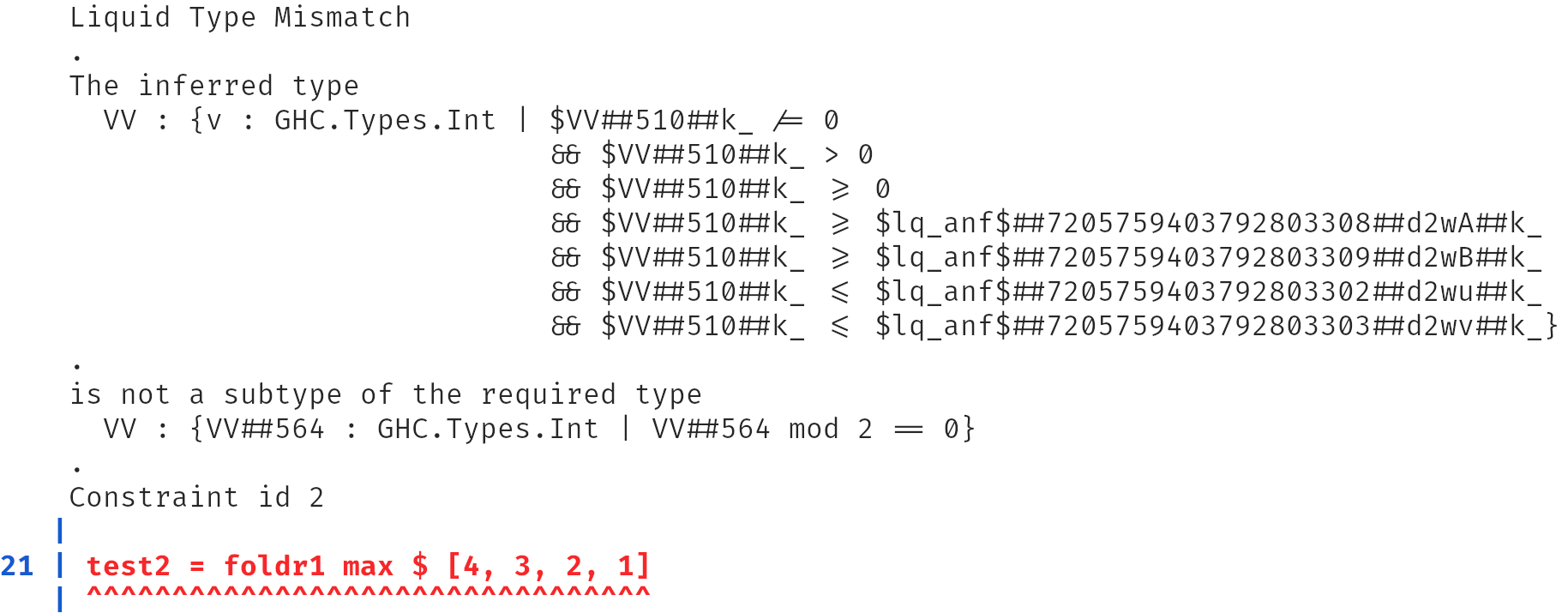
Summary: When refinement typing goes wrong, existing type-checkers offer little help.

Haystack

To make it easier to debug these and other verification failures, we built a new tool called Haystack, which makes it easier for users to debug verification failures. We describe Haystack and the theory behind it in a new paper which we wrote together with the incredible Ranjit Jhala and which was recently accepted at OOPSLA’24.

Haystack comes with a graphical user interface called Explorer, that lets the user interactively inspect typing violation. For our example, Explorer’s root screen displays the following.

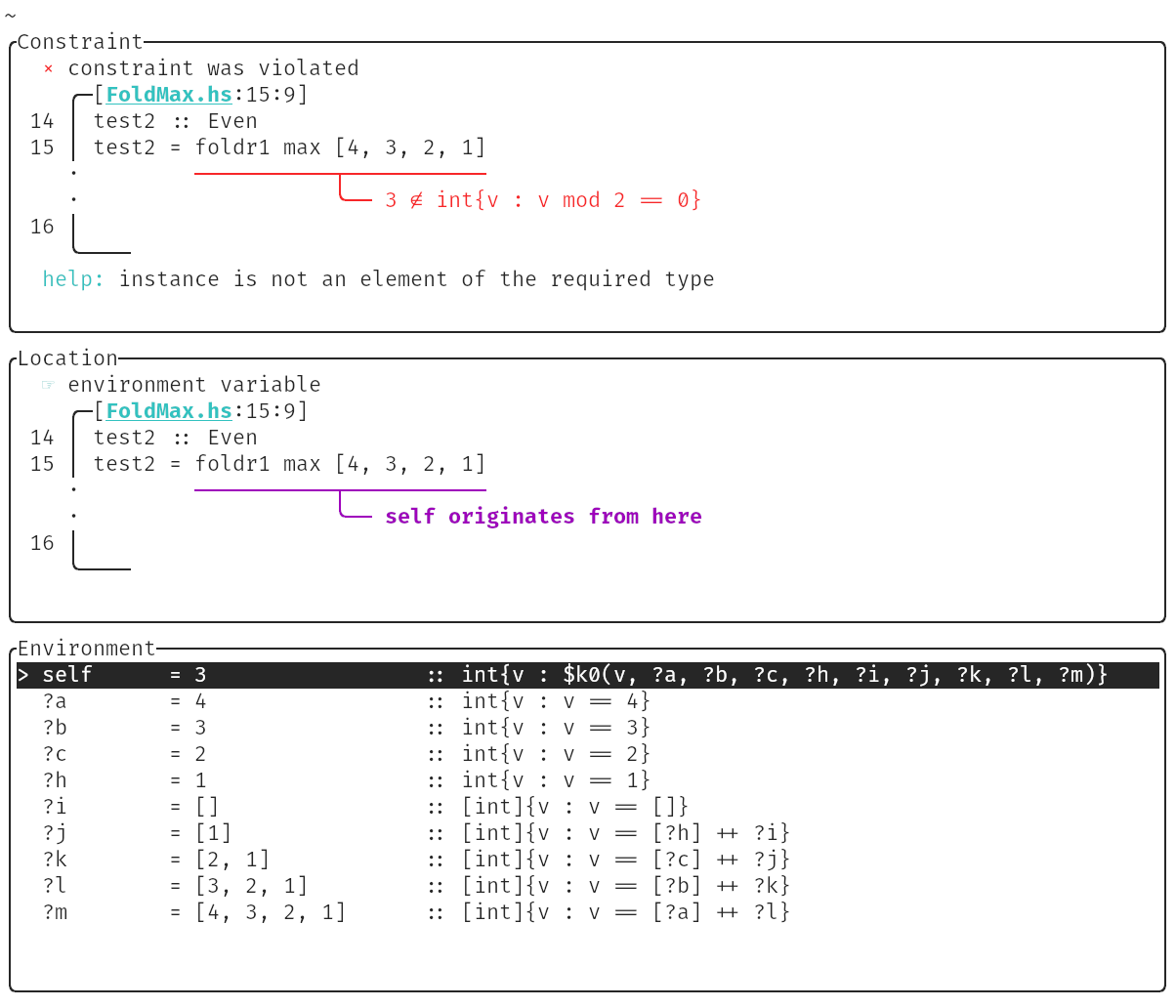
Indeed, the crucial piece of information comes from the requirement \(3 \not \in int\{v : v \; mod \; 2 == 0 \}\). The type signature of foldr1 requires the output type to be equal to the type of the list.

foldr1 :: (a -> a -> a) -> [a] -> a
foldr1 = ...

Since the output must be even, this means that every element in the list must be even. But that’s not true for \(3\), hence the type error.

Interestingly, the same thing that makes refinement typing so great – its modularity – is what makes it so hard to debug verifications failures. In fact, there is no program trace which could justify this verification failure. The program is correct, yet the failure is caused by the modular abstractions that come from the type system. That means, if we want to present a counterexample to the user, it must not be purely a counterexample to the property we want to prove, but instead, a counterexample to the typing derivation itself!

What even is a counterexample?

But that raises the question: what even is a counterexample to a typing derivation? That is, which mathematical object should we use to represent a failed typing derivation?

We answer this question in our paper with the notion of a refinement type refutation. We start from the bidirectional type system defined in this paper.

This type system defines two judgements. The first judgement \(\Gamma \vdash e \Leftarrow t\) says, under typing environment \(\Gamma\) expression e can be checked to have type \(t\). The second judgement \(\Gamma \vdash e \Rightarrow t\) says that under typing environment \(\Gamma\), we can synthesize a type \(t\) for expression e.

The difference between checking and synthesis comes from how we can use those judgements. For checking, \(t\) is an input to the typing rule, that is, we have to a supply a candidate \(t\) and the rule will check if, under a given typing environment \(\Gamma\) the expression can be typed against it. For synthesis, we only supply \(\Gamma\) and \(e\), and the rule produces a type as an output.

To define a notion of a failed typing derivation that matches the modularity of type-checking we now define two analoguous non-typing judgements. Judgement \(\Gamma \vdash e \not\Leftarrow t\) signifies a type-checking failure. The judgement says that we cannot check \(e\) to have type \(t\) under \(\Gamma\). Similarly, \(\Gamma \vdash e \not\Rightarrow \; !\) signifies a type synthesis failure. The judgement says that no possible type can be synthesized for \(e\) under \(\Gamma\).

Intuitively, a typing refutation contains two pieces of information. (1) a path towards a sub-expression with a failing subtyping check and (2) concrete variable instances that violate the constraint.

Refinement type refutations allow us to give a precise meaning to what it means to refute a type check. They form the theoretical underpinning for Haystack and are what we use to represent counterexamples. Indeed, our graphical tool Explorer lets the user browse exactly the refutation to the failed typing judgement.

Summary: Type refutations formalize the idea of a counterexample to a typing refutation. Haystack presents a graphical, interactive view of the type-refutation to the user.

Must Instantiations

An interesting complication in finding type-refutations comes from another strength of refinement type checking: refinement type inference, which allows for considerable automation.

Remember how we didn’t have to provide a type annotation for the refinement of foldr1?

Internally Liquid Haskell achieves this by assigning an unknown refinement to type variable a, and using a Horn constraint solver (called Liquid Fixpoint) to automatically generate a solution.

While unknown refinements are convenient for the user, they also make finding counterexamples hard. We now have to show that any possible solution for the unknown refinement will lead to a typing failure.

Haystack solves this problem via a new notion we call must-instantiation. To illustrate, in our example function test1, we know that any solution to the unknown refinement must at least contain inhabitant 3, as it is contained in the list [4, 3, 2, 1]. Since we also know that the unknown refinement must imply that all values are even, this alone is enough to ensure that any possible solution to the constraints must fail.

Summary: Must instantiations allow Haystack to refute typing judgement in the presence of refinement inference, which allows the user to omit intermediate type annotations. For this, must-instantiations specify values which must be part of any solution to the unknown refinements, yet violate a subtyping constraint.

Using Haystack

But does all of this really make proving programs correct easier?

Let’s look at a slightly more complicated example to convince ourselves that refinement refutations indeed do help.

Let’s say we want to write a simple expression evaluator.

An expression is recursively defined as a number, a variable, an addition, or a let definition. Instead of giving names to variables, we identify them by a natural number. Variable 0 is the most recently let bound variable; variable 1 the one bound before that, and so on.

This construction is similar to de Bruijn indices. We parametrize the data-structure by a type-variable a, which represents the type of values our expressions can take.

data Expr a
= ENum a
    | EVar Nat
    | EAdd (Expr a) (Expr a)
    | ELet (Expr a) (Expr a)

Next, we define an evaluator for these expressions. Our evaluator maintains an environment in the form of a list of values, which can be indexed by the identifier of an EVar.

We use function lookup to map variables to their value. The type of lookup ensures that the given identifier is indeed a valid index into the list.

lookup :: x:Nat -> [a]{v:x < len v} -> a

With this, we can define the evaluator. The helper function go recursively traverses the expression. The evaluation of an expression starts with an empty environment, and does all the things we would expect it to do.

It evaluates a number to itself, a variable to its value in the environment, an addition to the sum of evaluated expressions, and a let binding ELet e1 e2 by extending the environment with the value of e1 bound as the most recent variable identifier. So far so good.

eval :: Num a => Expr a -> a
eval = go []
where
    go _ (ENum i) = i
    go env (EVar x) = lookup x env
    go env (EAdd e1 e2) = eval env e1 + eval env e2
    go env (ELet e1 e2) = eval (eval env e1:env) e2

Unfortunately, our definition of eval is incorrect as it can produce out of bounds accesses to the environment. An expression can only be evaluated if it is closed, that is, if all variables are bound by a let expression.

HayStack locates the problem to lookup, specifically, it pinpoints the input env as violating its contract.

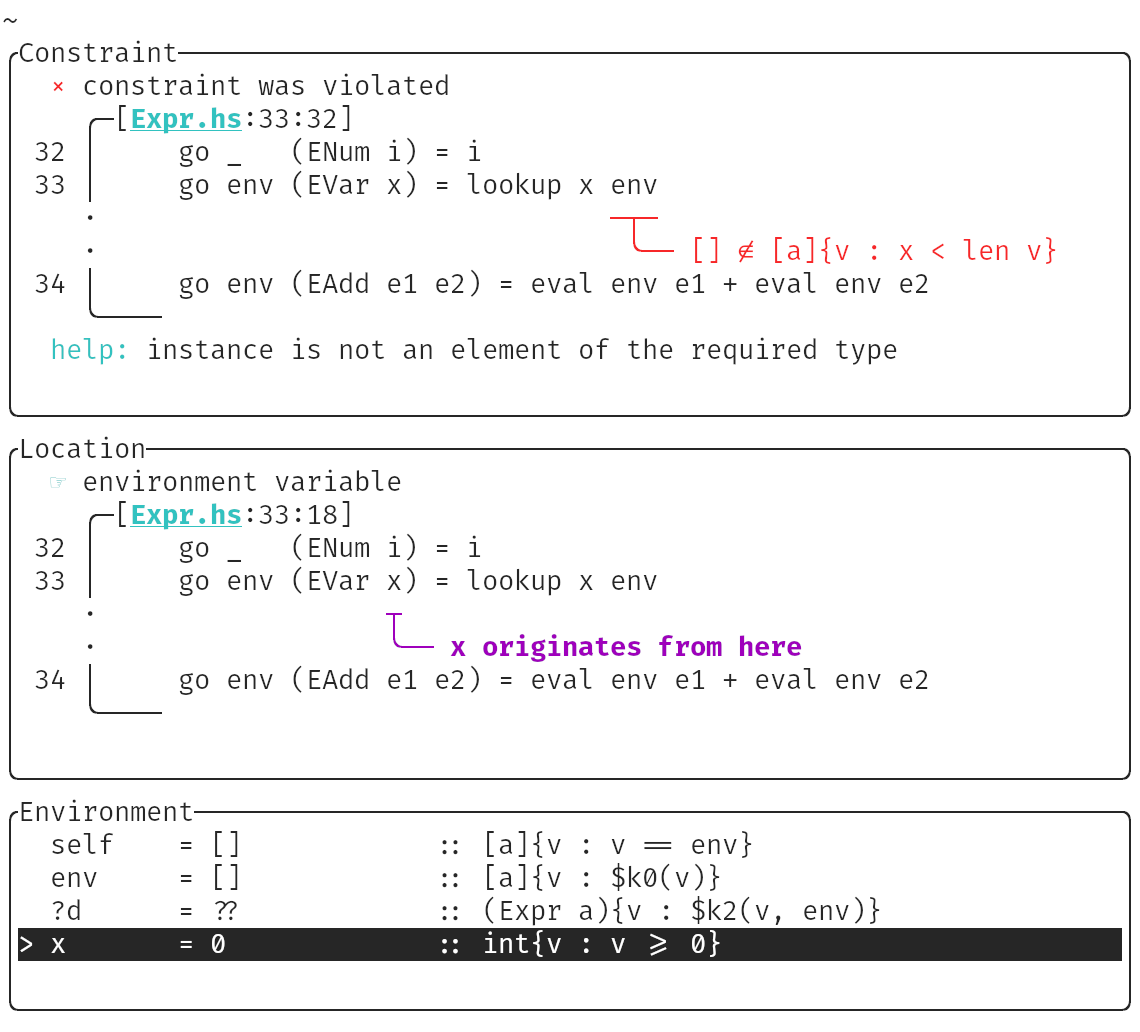
We can use Explorer to understand the root-cause of this violation. Below are two screenshots of the counterexample for eval, as produced by HayStack.

The first screenshot shows the top-level counterexample screen, which pinpoints the problem. It tells us we are trying to evaluate variable x in an empty environment. The bottom of the screen, displays variable bindings for the counterexample, which tells us that x is instantiated to 0. This leads to a violation of subtyping constraint displayed in red.

That is, the empty list [] is not a list whose length is strictly larger than x, which has value 0. Explorer also tells us which constraints were placed on x by the type checker, here that x is a natural number.

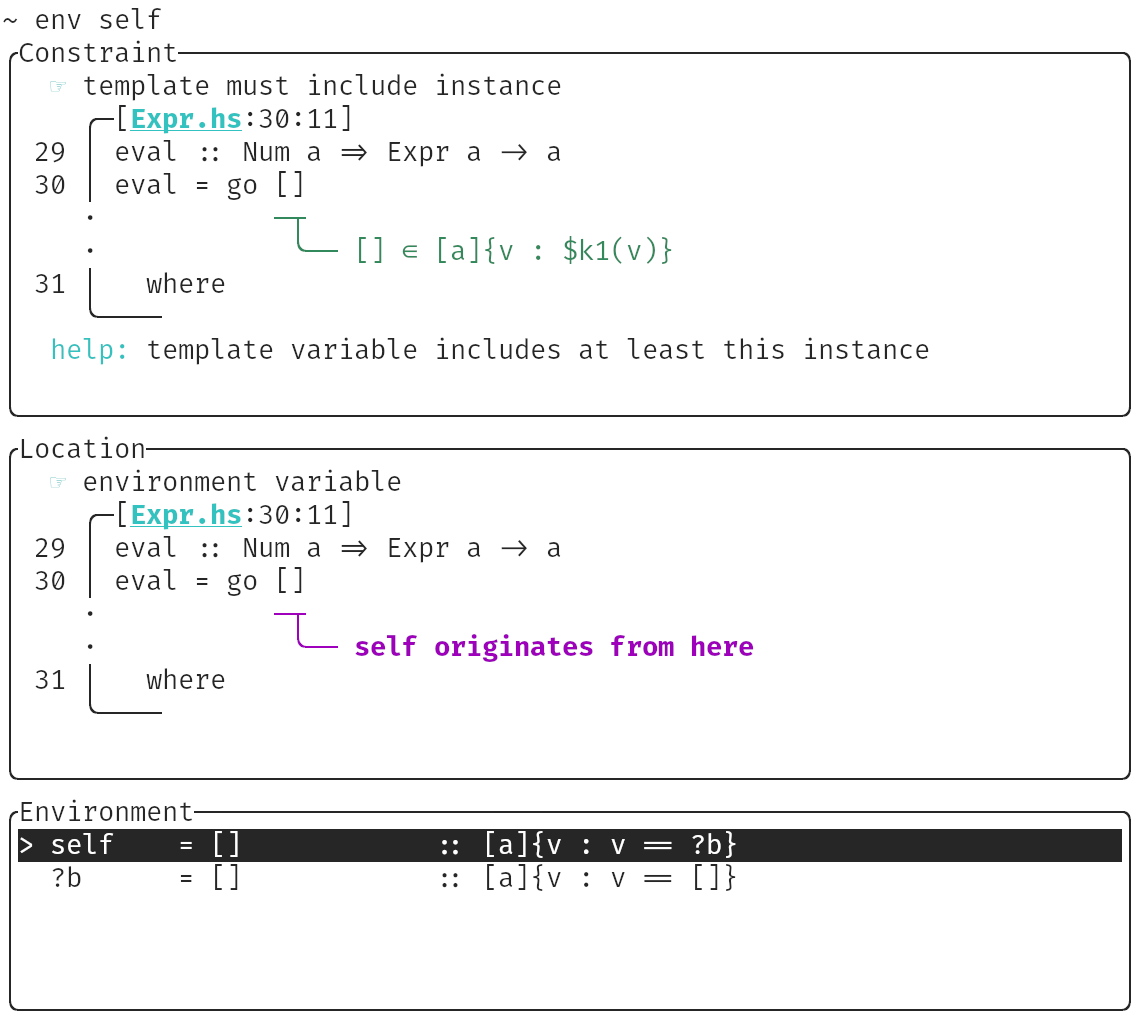
By clicking on env, we can get to the screen shown below. This screen displays more information about the unknown refinement for env, which shows us the origin of must-instantiation []. It comes from the top-level call to go in the definition of eval.

Using the counterexample, it becomes clear that eval should only accept closed expressions, which we can specify via a refinement.

Summary

To sum up, refinement type refutations offer a formalism to reason about typing violations, as well as a convenient way to represent violations to the user. Importantly, they follow the modular way of type checking itself, which often makes them smaller than traditional counterexample traces and lets us refute typing errors such as test2 above, where the program itself is correct, but the verification failure is a result of the abstractions imposed by the type system.

For more details, take a look at our paper, come to our presentation at OOPSLA’24, or download HayStack and give it a try.